Die Magie des Pentagram!

Das Pentagram als uraltes magisches Symbol symbolisiert die fünf Elemente. Neben den vier bekannten: Feuer, Wasser, Luft und Erde, als höchstes Element den (göttlichen) Geist. Eine ebenfalls gute Darstellungsform ist die Pyramide: vier Spitzen stehen auf der Erde, die fünfte jedoch zeigt nach oben.

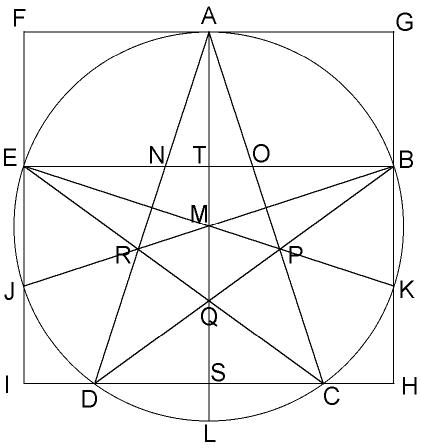
Ich glaube, dass in der gleichmaßigen Darstellung des Pentagrams eine mathematische Formel enthalten ist, die sich in irgendeiner Weise auf das Leben übertragen läßt. Um diese Formel zu finden, gehe ich von folgender Zeichnung aus.

Als Basis aller Berechnungen lege ich die Verbindung zweier Spitzen als Grundlänge a fest. Alle anderen Seiten werden zu dieser Seite ins mathematische Verhältnis gesetzt.

Die Berechnung der Winkel

Die Größen der Winkel im Pentagram lassen sich recht einfach ohne große Rechnerei über Winkelsummen und die Regeln der Wechselwinkel bestimmen. Wenn man alle fünf Geraden des Pentagramsin den Mittelpunkt M verschiebt, erhält man 10 gleich große Winkel, die zusammen 360 Grad ergeben. Folglich ist jeder Winkel für sich 36 Grad. Diese Winkel befinden sich an den Spitzen des Pentagrams (A;B;C;D;E). Die Verbindungen durch eine der Spitzen und den Mittelpunkt M teilen diesen Winkel in zwei zu 18 Grad.
Die Winkel an den Eckpunkten des Pentagons (N;O;P;Q;R) erhält man über die Winkelsumme in einem der Dreiecke, z.B. N,O,A. Die Summe der Winkel beträgt 180 Grad, der Winkel bei A beträgt 36 Grad. Also verteilen sich auf die beiden übrigen 144 Grad. Da die Winkel bei N und O gleich groß sind, muß jeder davon 72 Grad betragen. Interessanterweise doppelt so viel, wie der Winkel an den Spitzen.
Für die Innenwinkel des Pentagon ergeben sich 180 - 72 = 108 Grad. Das entspricht dem dreifachen des Winkels an den Spitzen. Zur Kontrolle: die Summe der Innenwinkel eines Fünfecks muß 540 Grad betragen (180 für die ersten drei Ecken und 180 für jede weitere Ecke).